几何问题是近年来国考数量关系的常考重点题型，且近几年国考中的几何问题的出题方向也不再局限于传统知识点的考查，更多的是考查考生的思维方法以及解决新题型的能力。因此，华图教育专家提醒考生朋友在备考过程中应对该问题引起足够的重视，做足充分准备，熟悉常考题型及常见解题思路，并且灵活运用常用方法解决新题型。当遇到使用常规思路和解题方法没有办法解决的问题时，考虑在时间充裕的情况下发散思维，多种角度思考该问题，找到快速的解题方法。下面我们就从题型和方法入手，回顾历年真题，并且给大家一些解决几何问题行之有效的方法。

  几何问题是行测考试中经常考查的部分，尽管大家在中小学都学过几何，但是行测考试中的几何问题与中学的几何问题相比，有自己的特点，重点是考查在复杂的问题中，如何迅速地得到答案。大家必须在掌握基础理论的同时，熟悉常考题型及其解法和技巧。

  1.基本公式类。一般运用基本的几何公式求解几何图形的边长、周长、面积、表面积、体积的几何变量。常考公式包括：圆形（圆弧，半圆，扇形）的周长公式，正方形、长方形、三角形、圆形（扇形）的面积公式，正方体、长方体的表面积公式以及正方体、长方体、球体、四面体和棱锥的体积公式。考生们需要牢记并且熟练运用以上公式，快速解决考查基本公式类的题目。

  2.割补平移类。顾名思义：割、补、平移。即我们在处理不规则的几何图形时一般会用“割补平移”的方法，将不规则图形转化为规则图形进行求解。

  3.几何特性类。几何特性类的题目通常考查三角形三边关系、几何最值问题、等比放缩类题目。这类题目难度不高，我们只需要记住一些固定的题型和基本结论即可轻松解决。

  4.新题型。近两年国考的数量关系都喜欢在几何问题上做文章，变换出题方式，着重考查考生的思维能力和解决非常规题型的能力。因此，在今年的国考备考中，我们要做好充足的准备，在时间充裕的情况下，尽量解决此类新题型。

  二、线）连接正方体每个面的中心构成一个正八面体（如下图所示）。己知正方体的边长为6厘米，问正八面体的体积为多少立方厘米?（ ）

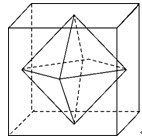
  分析：本题为立体几何问题，所求为一正八面体体积，属于基本公式类题目。但是我们没直接求解正八面体的体积公式，因此考虑将该正八面体沿中心平面分割为两个正四棱锥。如图下所示，每个四棱锥的底面为原正方体四个侧面的中心的连线，因此底面面积为正方体一个面面积的一半；高分别为上下两个底面中心到底面的距离。由棱锥体积公式有

  注释：考生还应了解基本的作图常识：“上北下南左西右东”，以及“北偏东”等基本概念。

  小结：基本公式类的题目总体上较为简单，我们只要依照题目所给条件及所求变量，再结合一些基本公式进行计算即可，在计算过程中认真仔细，避免运算上的错误。

  【例3】（2009-湖北-100）在下图中，大圆的半径为8，阴影部分的面积为（ ）？

  分析：观察上图我们得知：所求阴影部分为不规则图形，因此我们考虑采用“割补平移”的方法，将不规则图形转化为规则图形进行求解。如下图所示，连接四个小圆与大圆的切点及小圆之间的交点。我们按图中方式将阴影部分补成一个正方形，正方形的对角线，所以其面积：

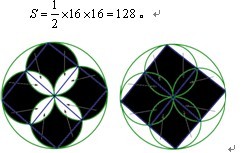
  小结：近几年的国考中虽没考查“割补平移”方法的运用，但是对不规则图形的求解作为一类重要的几何题型，其解题方法我们仍旧是应该熟练掌握的，我们在运用“割补平移”的办法来进行求解时要记住以下两个原则：

  2．当两个规则图形存在“包含”关系的时候，“大规则图形”挖去“小规则图形”所剩下的形状往往是不规则的，其面积必然是两个规则图形的差。

  【例4】（2008-国家-49）相同表面积的四面体、六面体、正十二面体及正二十面体，其中体积最大的是（ ）。

  分析：本题属于几何特性类题目。我们大家都知道：面积一定的图形，越接近于圆，则周长越小；周长一定的图形，越接近圆，面积越大。体积一定的图形，越接近于球，则表面积越小；表面积一定的图形，越接近球，则体积越大。本题四个选项中，正二十面体最接近球，因此体积最大。因此，本题选择D选项。

  注释：本题要注意A、B两个选项，四面体和六面体，由于其非“正”，故它们之间体积大小无法比较。

  【例5】(2010-国家-52)科考队员在冰面上钻孔获取样本，测量不同孔心之间的距离，获得的部分数据分别为1米、3米、6米、12米、24米、48米。问科考队员至少钻了多少个孔？

  分析：读完题目后可能很多考生不明白本题考查什么，如何下手，但是仔细分析后发现本题实质为：三角形三边关系的拓展。要想钻孔尽可能少，那么测量的6个距离的线段必须尽可能的构成的闭合回路，即必须使其他几条边的长度之和大于最长的边，而题目数据“1米、3米、6米、12米、24米、48米”中，任意一个长度都大于比它小的所有长度之和，故而这些线段不能构成闭合回路。因此，6个距离至少需要7个钻孔。

  小结：国考中对于几何特性类型题目的考查较少，且正常的情况下难度较低，因此，考生只需熟练掌握之前提到的三点：1.三角形三边关系；2.几何最值；3.等比放缩。就能很好的解决此类题目。

  【例6】（2012-国家-75）为了浇灌一个半径为10米的花坛，园艺师要在花坛里布置若干个旋转喷头，但库房里只有浇灌半径为5米的喷头，问花坛里至少要布置几个这样的喷头才可能正真的保证每个角落都能浇灌到?（ ）

  分析：如下图，读完题目后我们得知，本题不是一道常规的几何问题，而有点类似于构造问题。即要用半径为5米的小圆去覆盖半径为10米的大圆，且完全覆盖。此时，我们大家可以这样思考：既然是需要完全覆盖大圆，也就是大圆的圆周也要被小圆全部覆盖。而我们要怎么样用最少的小圆覆盖大圆的圆周呢？由之前的几何知识，每个小圆要想尽可能多的覆盖大圆圆弧，其覆盖的这段圆弧所对应的弦必为小圆的直径（如下图所示）。简单计算发现：由于每个小圆的直径为10，所以每个小圆至多盖住圆心角为60度相应的弧长，所以想盖住整个圆周，需要至少六个小圆，当且仅当这六个小圆以大圆的内接正六边形各边中点为圆心，但此时大圆的圆心未被盖住，所以至少需要七个圆。下面我们仅需给出一种七个圆的覆盖即可：以大圆圆心为圆心再放置一个小圆，我们计算后发现，其正好与其余六个圆相交如下图所示：

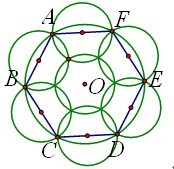
  小结：由本题我们大家可以看出，国考几何问题的题目越来越偏向于考查考生的思维能力及分析处理问题的能力。题目难度可能并不是很高，但要我们发散思维去进行思考。因此，建议考生在时间不是很充裕的情况下先放弃这类题目，当有时间剩余时再来解决。

  通过以上六道四类国考中几何问题的真题分析，我们得知在国考中，几何问题所占的比重还是很大的，且考查难度也是略有提升的，且题目类型也将会以新题型为主。但是我们解决新题型的能力亦是建立在对基本公式、基本方法的熟练掌握、运用的基础之上的，因此，广大考生需要熟练掌握基础题型的固定解法，并且提高思维能力和分析解决新问题的能力，从而做到游刃有余的解决国考中的几何问题。

  上海劳教人员解教控房价军令状恐落空65股龙卷风警卫员甘肃回应杨辉失学外交部驳安倍大兴摔童案二审鲜肺变黑报道不实菲律宾回应中国援助李天一案二审延迟退休缓冲期全会决定 三不写陈柏槐被调查揭秘国安委

• 上一篇: 【48812】通风管道按断面形状分有圆形、矩形两种。在相同的断面积下矩
• 下一篇: 【48812】其时视讯！圆柱的旁边面积公式是什么 相同适用于直圆柱和斜吗